Un famoso aneddoto racconta di come Johann Carl Friedrich Gauss (1777 -
1855), matematico, astronomo e fisico tedesco, all'età di 10 anni riuscì a stupire il suo
insegnante di matematica (J.G. Buttner).
Un giorno che gli studenti erano
particolarmente turbolenti, l’insegnante diede loro il compito di calcolare la
somma dei primi 100 numeri (da 1 a 100) pensando così di tenerli impegnati per
lungo tempo nell’eseguire un centinaio di somme. Dopo solo pochi minuti, il
giovane Gauss gli pose sotto gli occhi il risultato corretto (5050).
Probabilmente, si era accorto che,
mettendo in fila tutti i numeri da 1
a 100 e nella riga sottostante i
numeri da 100 a 1, ogni colonna dava come somma 101; Gauss fece dunque il prodotto 100 x 101 e divise per 2, o più semplicemente 50 x 101 ottenendo facilmente 5050.
Wikipedia riporta che probabilmente Buttner
aveva assegnato un compito ancora più complesso, ovvero la somma dei primi 100
numeri della serie 81297 + 81495 + 81693 ... nella quale ogni termine
differisce dal precedente per il valore 198 e che il giovane Gauss lo risolse
in pochi minuti come detto prima.
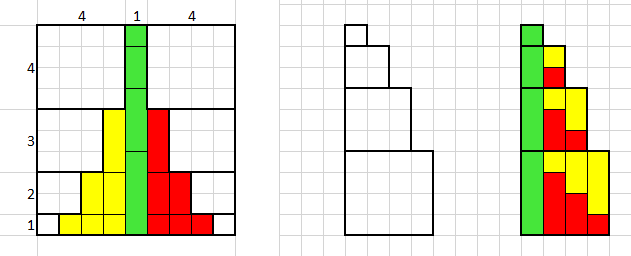
La seguente rappresentazione grafica
mostra in modo semplice come sistemando i valori in modo opportuno si ottengono
N colonne di valore N+1 e visto che ogni valore viene
contato 2 volte, si deve alla fine
dividere per 2, cioè:
N x (N+1) / 2
In questo caso si hanno 10 colonne di valore 11, per sommare i numeri da 1 a 10.
Al contrario di quello che normalmente
si crede, questo risultato fu però ottenuto 150 prima (nel 1631) dal matematico
Johann Faulhaber (1580 – 1635), che
calcolò anche le somme delle potenze di interi successivi:
In questa e altre formule intervengono i
numeri di Bernoulli Bn . Si osserva che la
somma delle potenze m-esime
dei primi n interi positivi è
data da un polinomio di grado m+1.
In effetti Carl Jacobi nel 1834 ha dimostrato che questa proprietà
vale per tutti gli interi positivi.
Le
singole formule possono essere ricavate per induzione o scrivendo sistemi di equazioni di grado m+1,
risolvendole per sostituzione.
Ad esempio per la somma dei primi n interi ipotizziamo che il risultato
sia del tipo:
a n2 + b n + c
Sostituendo n
con rispettivamente 0, 1 e 2 otteniamo:
c = 0
a + b + c = 1 >>>>> a
+ b = 1
4a + 2b + c = 3 4a
+ 2b = 3
da cui:
a = b = ½
e quindi la sommatoria risulta:
½ n2 + ½ n + 0 = ½ n (n + 1)
Per la somma di quadrati e cubi abbiamo
rispettivamente:
Mentre per le successive espressioni
polinomiali prosegue:
Esistono anche rappresentazioni grafiche della somma di
serie di quadrati o cubi.
Di seguito viene riportata la rappresentazione grafica
della sommatoria dei primi n quadrati:
12 + 22 + 32 + 42= 30
12 + 22+ 32 + 42 + 52 = 55
Come si vede utilizzando 3 serie di quadrati, e
combinandoli opportunamente, si ottiene un rettangolo i cui lati sono
rispettivamente:
“la somma degli interi da 1 a n” e “(2
volte n) + 1”
L'area di ogni serie di quadrati è quindi: N x (N +1) x (2N + 1) / 6
Il 6 e’ dovuto al fatto che nella somma da 1 a n e’
presente 1/2 e l’area va divisa per 3 (numero di serie
utilizzate).
Riporto infine un'altra formula notevole:
13 + 23 + 33 + … + n3
= (1 + 2 + 3 + … + n)2
http://en.wikipedia.org/wiki/Bernoulli_numbers
http://www.robertobigoni.eu/Matematica/FTrascendenti/f08/f08.htm
http://it.wikipedia.org/wiki/Somma_di_potenze_di_interi_successivi
http://en.wikipedia.org/wiki/Faulhaber%27s_formula